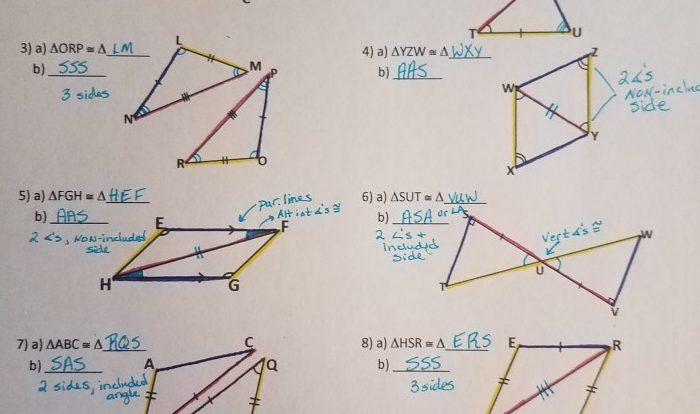
Chapter 8 Geometry Test Answers: Conquer Geometry with Confidence sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset.
Prepare to delve into the fascinating world of geometry, where shapes, angles, and theorems dance together in harmonious precision. This comprehensive guide will equip you with the knowledge and strategies you need to ace your Chapter 8 geometry test.
Chapter 8 Geometry Concepts
Chapter 8 of a geometry textbook delves into the fascinating world of geometric shapes and their properties. It introduces the fundamental concepts that lay the foundation for understanding more complex geometric principles in higher-level mathematics and real-world applications.
The chapter begins by exploring the basic geometric shapes, including points, lines, planes, triangles, quadrilaterals, and circles. Students learn about the properties of these shapes, such as their angles, sides, and areas. They also discover the relationships between different shapes, such as how to construct a triangle from a given circle or how to find the area of a parallelogram.
Polygons
Polygons are closed figures with straight sides. They are classified according to the number of sides they have, such as triangles, quadrilaterals, pentagons, and so on. Chapter 8 focuses on the properties of triangles and quadrilaterals, including their interior and exterior angles, side lengths, and diagonals.
Circles
Circles are closed figures with all points equidistant from a central point called the center. The chapter introduces the concepts of radius, diameter, circumference, and area of circles. Students learn how to calculate these measurements and explore the relationships between them.
Theorems and Postulates
Chapter 8 also introduces fundamental theorems and postulates related to geometric shapes. These include the Pythagorean theorem, which relates the lengths of the sides of a right triangle, and the postulates about parallel lines and angles. These theorems and postulates provide the foundation for proving geometric statements and solving problems.
Types of Geometry Test Questions
Geometry test questions come in various formats, each designed to assess different aspects of students’ understanding. Recognizing these types can help students prepare effectively and avoid common pitfalls.
Multiple-Choice Questions
Multiple-choice questions present students with a set of answer options for a given question. These questions test students’ basic knowledge and ability to identify correct answers from a limited pool.
- Example:Which of the following is the formula for the area of a triangle?
- (a) A = 1/2 bh
- (b) A = bh
- (c) A = 2bh
Common Pitfalls:Guessing, not reading the question carefully, and overlooking key details in the answer choices.
If you’re looking for a reliable source for chapter 8 geometry test answers, be sure to check out the resources available online. While you’re there, you might also want to explore pogil acids and bases answers to enhance your understanding of chemical reactions.
Don’t forget to come back for more chapter 8 geometry test answers if needed!
Short Answer Questions
Short answer questions require students to provide brief written responses, typically a few sentences or a short paragraph. These questions assess students’ ability to explain concepts, solve problems, and demonstrate their reasoning.
- Example:Find the length of the hypotenuse of a right triangle with legs of length 3 cm and 4 cm.
Common Pitfalls:Not showing sufficient work, making calculation errors, and failing to provide a clear and logical explanation.
Proof-Based Questions
Proof-based questions ask students to demonstrate their ability to construct logical arguments and prove mathematical statements. These questions require students to use axioms, definitions, and theorems to derive a conclusion.
- Example:Prove that the sum of the interior angles of a quadrilateral is 360 degrees.
Common Pitfalls:Not understanding the underlying concepts, making logical errors, and failing to provide a complete and coherent proof.
Strategies for Solving Geometry Problems
Approaching geometry problems strategically enhances your chances of finding solutions efficiently. This involves understanding the problem, drawing accurate diagrams, employing logical reasoning, deductive arguments, and utilizing problem-solving heuristics.
Understanding the Problem Statement
Thoroughly comprehend the problem statement. Identify the given information and what is being asked. Break down complex problems into smaller, manageable parts. Translate verbal descriptions into mathematical equations or diagrams.
Drawing Accurate Diagrams
Diagrams provide visual representations of the problem. Draw them accurately, labeling all relevant information. Diagrams help visualize relationships between objects and identify patterns.
Logical Reasoning and Deductive Arguments
Use logical reasoning to deduce new information from given facts. Deductive arguments allow you to draw conclusions based on premises. Start with known information and apply geometric theorems, properties, and postulates.
Problem-Solving Heuristics, Chapter 8 geometry test answers
Employ problem-solving heuristics to guide your approach. These include:
- Guess and Check:Make an initial guess and systematically test its validity.
- Working Backward:Start from the desired conclusion and work backward to find the necessary steps.
- Analogy:Relate the problem to a similar one you have solved before.
Common Errors and Misconceptions: Chapter 8 Geometry Test Answers
In Chapter 8 geometry, students often encounter errors and misconceptions that hinder their understanding. Identifying and addressing these misconceptions is crucial for improving comprehension and problem-solving abilities.
Common errors arise due to several factors, including insufficient conceptual understanding, lack of practice, and misconceptions carried over from previous concepts. To avoid these errors, students should focus on building a strong foundation, practicing regularly, and seeking feedback to clarify any misconceptions.
Error 1: Confusing Similar and Congruent Figures
Students often confuse similar figures with congruent figures. While similar figures have the same shape but not necessarily the same size, congruent figures have both the same shape and the same size. This error can lead to incorrect conclusions about angles, side lengths, and other geometric properties.
To avoid this error, students should remember that congruence implies both shape and size equality, while similarity only implies shape equality. They should also practice identifying and classifying figures as similar or congruent.
Error 2: Incorrect Application of Angle Sum Theorems
Students may make errors when applying angle sum theorems, such as the triangle angle sum theorem and the exterior angle theorem. These errors can result from forgetting the theorems or misapplying them to non-applicable cases.
To address this error, students should memorize the angle sum theorems and practice applying them to various types of triangles. They should also be aware of the conditions under which these theorems are applicable.
Error 3: Misunderstanding Pythagorean Theorem
The Pythagorean theorem is often misunderstood or misapplied. Students may forget the formula or use it incorrectly, leading to incorrect answers. Additionally, they may not understand the relationship between the sides of a right triangle and the theorem.
To avoid this error, students should memorize the Pythagorean theorem and practice using it to solve problems. They should also understand the geometric relationships between the sides of a right triangle and how they relate to the theorem.
Preparation Tips for a Geometry Test
Geometry can be a challenging subject, but with the right preparation, you can succeed on your Chapter 8 geometry test. Here are some tips to help you get started:
Review your class notes.This is the best way to make sure you understand the concepts that will be covered on the test. Pay attention to any examples or practice problems that your teacher has gone over in class.
Complete practice problems.The more practice problems you complete, the better prepared you’ll be for the test. You can find practice problems in your textbook, online, or in your teacher’s handouts.
Seek help when needed.If you’re struggling with a particular concept, don’t be afraid to ask your teacher or a tutor for help. They can help you understand the concept and answer any questions you may have.
Effective study habits.When studying for your geometry test, it’s important to use effective study habits. This means setting aside a specific time each day to study, finding a quiet place to study, and avoiding distractions.
Time management strategies.On the day of the test, it’s important to manage your time wisely. Make sure you arrive at the test on time and give yourself plenty of time to complete the test. Don’t spend too much time on any one question, and if you’re not sure about an answer, guess and move on.
Practice Questions and Solutions
Solving geometry problems requires practice and a deep understanding of the concepts. Here are some practice questions with detailed solutions to help you master the subject.
These questions cover a mix of multiple-choice, short answer, and proof-based questions. Each solution includes step-by-step explanations and clear reasoning.
Multiple-Choice Questions
- Which of the following is not a property of a rectangle?
- Opposite sides are parallel.
- Diagonals are equal in length.
- Angles measure 90 degrees.
- Find the area of a triangle with a base of 6 cm and a height of 4 cm.
- 12 cm²
- 24 cm²
- 48 cm²
Short Answer Questions
- Define the term “similar triangles.”
- Find the length of the hypotenuse of a right triangle with legs measuring 3 cm and 4 cm.
Proof-Based Questions
- Prove that the sum of the interior angles of a quadrilateral is 360 degrees.
- Prove that the diagonals of a rhombus are perpendicular bisectors of each other.
FAQ Insights
What are the key concepts covered in Chapter 8 of geometry?
Chapter 8 of geometry typically covers topics such as quadrilaterals, circles, triangles, and their properties, as well as theorems like the Pythagorean theorem and angle relationships.
What are some common types of questions on a Chapter 8 geometry test?
Geometry tests often include multiple-choice questions, short answer questions, and proof-based questions that assess your understanding of geometric concepts and your ability to apply theorems and solve problems.
How can I prepare effectively for my Chapter 8 geometry test?
To prepare effectively, review your class notes, complete practice problems, and seek help from your teacher or a tutor if needed. Focus on understanding the concepts and practicing different types of questions to build your confidence.